〒981-0933 仙台市青葉区柏木1-2-29-301
電話での受付:15:00~20:00
定休日:日曜日
受験数学の素朴な疑問に答える
学校で教わる数学をやっていて、「どうしてこうなんだろう?」「なぜこうなっているんだろう?」という疑問をお持ちになったことのある方は多いと思います。
以下は、わたしが現役受験生の際、数学の学習において、「どうしてこうなんだろう?」「なぜこうなっているんだろう?」と感じたことに対し、自ら咀嚼した上で回答を記したものです。
わたしはプロフィールにある通り、数学の専門ではありません。
他方、10余年の宮仕えの経験があり、数学が実際の社会でどのように使われているかを体験する機会を持ちました。
それを基にすれば、数学の専門家とは違った視点で数学をとらえることができると考えます。
数学の3原則
ここで、わたしが考える数学の3原則を挙げます。
1.数学の目的は、我々が楽をするために編み出されたものである。
2.数学の諸分野は「こんなこといいな。できたらいいな」と誰かがどこかで考え、「じゃ、新しく作っちゃえ」としたものの集大成である。
3.数学の問題解法の鉄則は、上掲の目的を達するため、「3つのものを2つにして考える」「2つのものを1つにして考える」というように、できるだけ簡略な形にして考える。
数学の第1原則 〜我々が楽をするために〜
数学とは、我々が楽をするために編み出されたものです。
ここでいう「楽をする」というのは、「少ない情報を手掛かりに多くの情報を手に入れることができる」という意味です。
例えば、
という三角形の区画にペンキ塗りの工事作業をすることを考えます。
ここで、この三角形の面積が計算で出るなら、作業の前に「必要なペンキの量はどのくらいか」「必要な作業員の数はどのくらいで、時間はどのくらいかかるか」というおおよその情報を得ることができます。
面積を計算せず、行き当たりばったりで作業をすれば、時間・かかるお金に大きな損失が出てしまいます。
こうした損失を未然に防ぐため、この三角形の面積を計算するには、(高さ)と(底辺)という「2つの情報」を得れば、(面積)=(底辺)×(高さ)÷2となり、それだけ楽をすることができます。
また建築現場で、
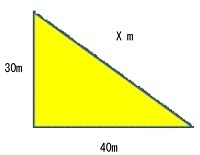
右図のXを求めようとした場合、三平方の定理により、X=50mと計算で求めることができ、わざわざ測量しなくてもよくなります。
よって作業が簡便かつ迅速になり、「楽をする」ことができます。
以上のように、数学のおかげで、わたしたちはよりよい生活を送れるのです。
数学の第2原則 〜目的のために新しいことを作る〜
数学の諸分野は「こんなこといいな。できたらいいな」と誰かがどこかで考え、「じゃ、新しく作っちゃえ」としたものの集大成です。
こういうのを見ると、世の中にはつくづく頭のいい人がいるものだと感嘆しきりです。
こうした集大成の中には、1より小さい数を10等分単位で表すことを目的とした小数のように「作った意味が分かりやすい」ものもあれば、平方根、ベクトル、虚数のように「なぜこういうものが必要なの?」と感じるものもあります。
学年が進むほど「なぜこういうものが必要なの?」という分野は多くなります。
数学の第3原則 〜なるべく簡略な形に〜
数学の問題を解く際は、「3つのものを2つにして考える」「2つのものを1つにして考える」というように、できるだけ簡略な形にして考えるというのが原則です。
例えば、秒速10mと時速20kmはどちらが速いかという問題では、「秒速と時速」「mとkm」は単位が違っているため、単純比較できません。
そこで両方の単位をそれぞれ「時速とkm」に換算して比較します。
「秒速と時速」という2つの要素を1つに、「mとkm」という2つの要素を1つにするという原則がここで生きています。
また
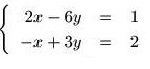
というような連立方程式はXおよびYという2つの文字よりなる式の中で、XまたはYのいずれかの文字を消し、一方の文字の値を求めてから、他方を確立させます。
ここにも「2つのものを1つにして考える」という原則が生きています。
四則混合算はなぜ掛け算・割り算を足し算・引き算に優先させるか
5+6×3の答えを求めよ、という問題が出されると、5+6×3=5+18=23となり、掛け算・割り算は足し算・引き算に先んじて計算すべしと教えられます。
理由は説明されません。
「数学の約束」ということになっています。
ここでどうしてそういう約束があるのかを考えると、1つの結論に達します。
もし、上記のような約束がなければ、
2a+4a=6a
という計算ができなくなってしまうのです。
上の計算は、中学1年生で出てくるごく基本的なもので、何の気なしに計算して答えを出していますが、それもこれも「掛け算・割り算を足し算・引き算に優先させる」という約束があればこそできるのです。
なぜなら、
2a+4a=2×a+4×a
なので、
この約束がなければ、
2a+4a=2×a+4×a=(2a+4)×a=2a^2+4a(^は累乗を意味します)
などという答えも可能になってしまいます。
それでは不都合極まりないことです。
この「掛け算・割り算を足し算・引き算に優先させる」にもこうした深いわけがあるのです。
零=0は「何もない」という意味ではなく、「基準点」と考える
「あなたの点数は0点です」「わたしの取り分は0です」と言えば、通常「何もない」ことを意味します。
しかし数学では0=「何もない nothing」という意味では必ずしもありません。
例えば、気温0℃というのは、「気温がない」という意味ではありません。
この0℃は水の融点ですから、0=「何もない」ということではなく、「基準点」という意味です。
とすれば、−1℃が「基準点」より1℃下回る温度になるというのも納得がいきます。
マイナスの数の効用 〜数が「小さく」なって、「分かりやすく」なる〜
上記で0(零)は「何もない」という意味のみならず、「基準点」であることも学びました。
それを受けて、マイナスの数をここで登場させます。
ここで0を「基準点」、「基準点」を下回る数をマイナス、「基準点」を上回る数をプラスと定義します。
すると、数が一気に小さくなって、計算しやすくなります。
以下の例を見てください。
<表①>
| 国語 | 数学 | 理科 | 社会 | 英語 |
| 82 | 81 | 75 | 77 | 84 |
この点数につき、80点を基準すなわち0と考えると、<表①>は次のように変身します。
<表②>
| 国語 | 数学 | 理科 | 社会 | 英語 |
| 2 | 1 | −5 | −3 | 4 |
こうすることで、2ケタの数が1ケタに化けます。
いま、5教科の平均を求めてみます。
①より
(82+81+75+77+84)÷5=79.8
ここで②の表を使うと2+1−5−3+4=−1
80点を基準としているので、平均は80−1/5=79.8となり、計算が容易です。
以上のごとく、マイナスという概念を使うことで、数が小さくなり、より「簡単に」なるのです。
0で割ることができない理由
小学校で習う通り、
0÷3=0
となりますが、
3÷0
の答えは存在しません。
そうなる理由は以下のように説明されます。
リンゴ0個を3人で等分すると、1人当たりのリンゴの数は0個です。
ないものは等分しても0ですから、
0÷3=0
です。
また、リンゴを0人で等分すると、1人当たりのリンゴの数は.....
分配すべき人が誰もいないのに、「1人当たりのリンゴの数」は計算できませんから、3÷0の答えは存在しません.....
というのが根拠です。
小学校のうちは3÷0を計算せよ、などという計算問題は出ることはありませんが、(ひねくれた数学の先生であれば、「解なし」という答えをもって「正解」とする、ということは考えられなくもないですが.....)注意すべきは特に高校以降の数学です。
数式を扱う際には、分母=0とならないように場合分けをするなど、しかるべき処理をしなくてはなりません。
ここで分母=0にからんで興味深い教科書の記述があります。
中3に出てくる2次方程式のところで、以下のような問いが出てきます。
<問題>
X^2+4x=0を解け
◎解法
X^2+4x=0
x^2= -4X
両辺をXで割って
解は
X=−4
→この解法の誤りを指摘せよ
「教科書ガイド」に掲載されていた本問に対する模範解答は以下のとおりです。
<解答>
両辺でXを割るのは、X=0の場合も含まれるため不可。
よって左辺=0にして以下のようにして因数分解して解を得る。
X^2+4X=0
X(X+4)=0
X=0, X=−4
この模範解答において、X=0の場合が含まれるというのはそのとおりですが、X=0の場合が含まれるから因数分解をしないと解が得られないということはありません。
実はこの方程式は因数分解を用いなくとも解けます。
解き方は以下のとおりです。
X^2+4X=0
X^2=−4X
(ア)X≠0のとき
両辺をXで割って X=−4
(イ)X=0のとき
X=0を両辺に代入してもこの式は成り立つので、これも解。
以上より、
X=0, X=−4
平方根は何のためにあるの? 〜二次方程式が解けるといいな〜
平方根にはいろいろな使い道があります。
その中で大きいのが、二次方程式の解を「簡単な形」で表すことができるということにあります。
では、二次方程式が解けるとどのような「よいこと」があるのでしょうか。
応用範囲は非常に広いですが、ここでは、上掲の図を再び使って説明します。
<図1>
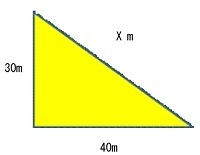
ここで、<図1>のXは三平方の定理より
X^2=40^2−30^2=2500
X>0より
X=50です。
<図2>
![pitaq01[1].gif](/_p/acre/26082/images/pc/9d7d0f54.gif)
<図2>においては
X^2=2×2−1×1=3
X>0より
X=√3となります。
これでXの箇所は実際に測量する必要がなく、計算ができるので、楽をすることができます。
もっとも√3はどういう数だか分からず、近似値として
√3=1.730508.....
という数が与えられており、実務上はそちらを使います。
実務の上では近似値を使うのに、数学で根号を用いるのにはいくつかの理由があります。
ここでは2つ挙げます。
第一に、数学はあくまで基礎理論であって、数学という論理上の正確さは求められても、実務の上でいかにそれを応用・利用するかについては、思考の範疇の外にあるからです。
早い話、数学は「理屈」が正しければよく、実務でどう使うかということまでは想定していません。
第二に根号を使うことで、
√48+√12=4√3+2√3=6√3
√10×√15=5√6
のように「より簡単な形」にまとめることができるということです。
ということは、近似値を求める際にも、より正確な近似値が出ます。
例えば
√10=3.162277660
√15=3.872983346
√6=2.449489743
とすると、
√10×√15=3.162277660×3.872983346=12.247448714
5√6=5×2.449489743=12.247748715
となり、小数点の端数を考えると計算するのも楽ですし、より理論値に近いものが求められます。
三角関数はなぜああいう「決め方」をしたのか 〜2つのものを1つで管理〜
高校生になると、数学で三角関数を取り扱います。
この分野に入ると、多くの生徒さんが困惑します。
というのも、sin, cos, tanがなぜこのような決め方をしたのか、教科書には書いていないからです。
まず、三角関数のsin, cos, tanの意味は、単位円において
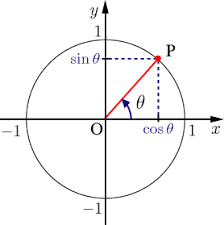
となるように、
cosθはX座標そのもの
sinθはY座標そのもの
tanθは直線OAの傾きそのもの
を表します。
三角関数の要諦は、「三角関数を仲立ちにして、平面上の任意の点を一括管理できる」ということです。
例えば、(3,4)という点は、上手のように(3,4)=(5cosθ,5sinθ)とすることができます。
X=3、Y=4という全くバラバラな数が、それぞれ、三角関数の中に組み込まれます。
(3,4)=(5cosθ,5sinθ)となると、
sinθ^2+cosθ^2=1
という公式を使って、sinθもしくはcosθだけで表すことができます。
ということは、(X,Y)=(3,4)という、X・Yそれぞれバラバラな数字が、三角関数を仲立ちにして一括管理できます。
一括管理できるということは、2つのことを1つにまとめて考えることができ、それだけ楽ができるのです。
しかも
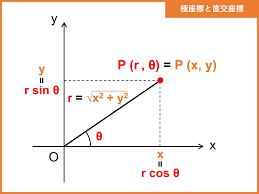
という公式を使えば、当該(X,Y)の点と原点との傾きまで求められます。
さらにθを動かすことで、点や線、回転移動、平行移動もより容易に考えることができます。
この分野はベクトルや行列と特に関係の深い分野です。
三角形の辺も併せて一括管理 〜余弦定理〜
三角関数において、その効用は、平面上の任意の点(X,Y)を一括管理できることにあると述べました。
ここで、余弦定理を使うと、三角形の辺も三角関数で一括管理できます。
一括管理できるということは、2つのことを1つにまとめて考えることができ、その分だけ楽ができます。
上図においては、辺a,b,cからcosBの値が出て、よってBの値が出ます。
同様にして他の角も出てしまうという使い勝手のよい公式です。
この公式は加法定理にも応用されるなど、幅広く使われています。
お気軽にお問合せください

メール・お電話でのお問合せ
<電話での受付>
15:00~20:00
※日曜日は除く
※電話は
「雅興産(みやびこうさん)」と出ます
成績upのヒント!
教育コラム「雨か嵐か」
プロ家庭教師菊池
住所
〒981-0933
仙台市青葉区柏木1-2-29-301
電話受付時間
15:00~20:00
定休日
日曜日

