平方根にはいろいろな使い道があります。

その中で大きいのが、二次方程式の解を「簡単な形」で表すことができるということにあります。

では、二次方程式が解けるとどのような「よいこと」があるのでしょうか。

応用範囲は非常に広いですが、ここでは、上掲の図を再び使って説明します。

＜図１＞

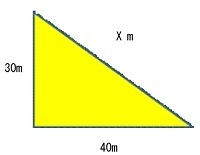
ここで、＜図１＞のＸは三平方の定理より

Ｘ^２＝４０^２−３０^２＝２５００

Ｘ＞０より

Ｘ＝５０です。

＜図２＞

＜図２＞においては

Ｘ^２＝２×２−１×１＝３

Ｘ＞０より

Ｘ＝√３となります。

 

これでＸの箇所は実際に測量する必要がなく、計算ができるので、楽をすることができます。

もっとも√３はどういう数だか分からず、近似値として

√３＝１．７３０５０８.....

という数が与えられており、実務上はそちらを使います。

実務の上では近似値を使うのに、数学で根号を用いるのにはいくつかの理由があります。

ここでは２つ挙げます。

第一に、数学はあくまで基礎理論であって、数学という論理上の正確さは求められても、実務の上でいかにそれを応用・利用するかについては、思考の範疇の外にあるからです。

早い話、数学は「理屈」が正しければよく、実務でどう使うかということまでは想定していません。

第二に根号を使うことで、

√４８＋√１２＝４√３＋２√３＝６√３

√１０×√１５＝５√６

のように「より簡単な形」にまとめることができるということです。

ということは、近似値を求める際にも、より正確な近似値が出ます。

例えば

√１０＝3.162277660

√１５＝3.872983346

√６＝2.449489743

とすると、

√１０×√１５＝3.162277660×3.872983346＝12.247448714

５√６＝５×2.449489743＝12.247748715

となり、小数点の端数を考えると計算するのも楽ですし、より理論値に近いものが求められます。