〒981-0933 仙台市青葉区柏木1-2-29-301
電話での受付:15:00~20:00
定休日:日曜日
中3生 1学期の評定と学年評定 ~どう違ってくる?~ その1 2024/11/01
今日から11月です。
中3生の多くが今月に定期試験を控えています。
11月中旬までに定期試験→11月下旬までに評定が決定
という流れが一般的です。
今回のコラムでは、1学期に出た評定と、11月下旬までに出る評定との関わりについて述べてみます。
結論を申しますと、
「1学期に出た評定と11月に出る学年評定とで数字はほぼ変わらない」
です。
ですから、10月に1学期の評定として出た数字が、実質的に「3年生の学年評定」になります。
ただ、これまでは、10月に出た「1学期の評定」と、11月下旬までに出る「3年生の学年評定」とで、少し数字が変わったケースがありました。
変化があるのは、全体の2割程度の生徒さんです。
統計を取ったわけではないので、この数字はわたしの記憶に基づいたものです。
数字として変わるのは、1科目1上がる・1下がるくらいでした。
「数字はほぼ変わらない」と先ほど書いたのは、そのためです。
ただ、9月までの定期試験と、11月の試験とで点数が大きく上がったり、下がったりした場合、当然に評定の数字は変わってきます。
とはいえ、「大きく上がる」ことはほぼないでしょう。
心配なのは、「大きく下がる」ことです。
(次回に続きます)
中3生 1学期の評定と学年評定 ~どう違ってくる?~ その2 2024/11/02
(前回の続きです)
ここでご留意いただきたいのは、
「多くの学校の先生方はできることなら良い成績を付けたいと思っている」
ということです。
もちろん、そのように考えない先生もいらっしゃるはずです。
ただ、多くの先生方には、生徒さんに対する思い・優しさのようなものがあるような気がしています。
これは、わたしが生徒さんの評定の数字を見ていての感想です。
「良い成績を付ける」といっても、もちろん基準というものがあります。
それを踏み越えてということはできません。
しかし、多くの先生方は「できることなら良い成績を」とお考えであることは、何となく伝わってきます。
事実、10月に出た「1学期の評定」と、11月下旬までに出る「3年生の学年評定」とで、「数字が変わった」生徒さんは、数字が上振れしているケースが多い印象を受けています。
上振れしているのは、実技教科が意外と多かった記憶があります。
まあ、何はともあれ、3年生の学年評定が出てくるのは、もうすぐです。
特に志望校の平均的な評定に達しない生徒さんは、入学まで落ち着かない日々を送ることになります。
受験までは、生徒さん・ご父兄・受験関係者の二人三脚がなるべく乱れないよう、過ごしていきたいものです。
動画「仙台圏公立高校 中退率 ベスト3 ワースト3」の補足 その1 2024/11/03
過日、表題にあるYouTube動画をアップしました。
上に示した動画では、ベスト3・ワースト3のみを発表しました。
ランク表は次のようになっています。
このランク表に関して、わたしなりの考察を加えます。
まず、最も中退率率の低かったのが、仙台工業というのは、正直、意外な感じがしました。
わたしの事前の予想では、
「難易度が低くなると中退率が高くなる」
といったものでした。
ですから、ナンバースクールは中退率が低く、偏差値順にランク表がきれいに並ぶと考えていたのです。
数字を見ると、そういう傾向はなくはありません。
が、「きれいに並んでいるか」と言われれば、決してそうではありません。
三高が2位で、二華が3位というのは、何となく合点がいきます。
一高が4位というのも、順当なところでしょう。
ただ、宮一が28校中20位で、中退率が4.6%です。
この数字は、平均値4.0%を上回っています。
そして、人数にして13名が中退者です。
13名の中退者というのは、決して小さくない数字です。
宮一の難易度を考えると、かなり意外な感じがしました。
(次回に続きます)
動画「仙台圏公立高校 中退率 ベスト3 ワースト3」の補足 その2 2024/11/04
(前回の続きです)
わたしが意外に感じたのは、泉館山・向山・宮城野といった高校の中退率です。
この3校は、偏差値でいえば、55~60というところに位置しています。
それがいずれも中退率5%を超えています。
これがいつものことなのか、通常とは違っているのか、そのあたりのことはよく分かりません。
何かの機会に調べてみようとも思いますが、それにしても...という気はします。
わたしがこれら3校に描いたイメージは、
「ナンバースクールよりはほんの少し高いかもしれないが、誤差の範囲だろう」
というものです。
ところが、当初の予測に反して、意外なほどの中退率の高さです。
そして青陵の数字の高さも気になります。
こちらに関しては、今回の動画に寄せられたコメントによれば、学校が
「高校から公立高校受験は控えてほしい」
というプリントを出すそうです。
こういうのが出されるというのは、それだけ青陵から公立高校受験をする生徒さんがいるということなのでしょう。
もちろん、青陵中を中途で抜けていった生徒さん全員が、高校受験をするわけでないとは思います。
純然たる学業不振などが理由というケースもあるでしょう。
いずれにしても、いろんなことが見えて、勉強になりました。
数学 トップ層のミスと下位層のミス ~その違い~ その1 2024/11/05
これまで、数学のミスについては、当コラムで何度か取り上げてきました。
今回は、それをさらに掘り下げてみます。
そして、数学という教科に関して、成績優秀者であるトップ層のミスと、そうでない下位層のミスを比べてみます。
それらを比べてみることで、受験学習はどのようになればよいのか、ヒントになります。
<トップ層のミス>
・ミスが少ない
・ミスは答えが出る直前にやらかすケースが多い
・ミスをする箇所は「小1・小2レベルの算数」であることが意外に多い
<下位層のミス>
・ミスが多い
・ミスは計算の導入部分・最初のほうですでに起きていることが多数
・当人は「単なるケアレスミス」と考えているが、ほとんどはそもそもの理解不足より起きる
「トップ層はミスが少なく、成績が下に向かうにつれ、ミスが多くなる」
これについては、異論がないでしょう。
そうした中で、ミスの起きる箇所には、両者で大きく差があるように感じます。
トップ層のミスは、「あともう少しで答えが出る」というところで起きているパターンが多いです。
しかもそのミスは、小1・小2レベルのごくごく簡単な計算です。
「この問題は解けたから、あとは次に行こう」
などと考えながらやっていて、思わぬ場所でつまずいてしまうということなのでしょう。
(次回に続きます)
数学 トップ層のミスと下位層のミス ~その違い~ その2 2024/11/06
(前回の続きです)
一方、下位層のミスは問題を解くときの取っ掛かりの時点で間違っていることが多い印象を受けています。
そのミスとは、
・問題文を正確に理解できていない
・計算のルールを理解できていない
・問題文を読むときにしても、計算にしても、答案のところに書けばいいものを、書かずに済ませて間違う
そして、こうしたミスを少なくするにはどうすればよいかという話になります。
トップ層のミスというのは、前回のコラムで述べたとおり、答えが出る直前の「小1・小2レベルの算数」であることが多いです。
例えば、ルートやら分数やらの計算を途中まで誤りなくしてきて、最後の最後で、
2+3=6
とするような間違いです。
こうしたものをなくすには、
「最後の最後まで気を抜かない」
「易しいものほど慎重に対応する」
という姿勢を常に持って問題に臨む以外にないものと思われます。
事実、過去にこのような生徒さんを担当し、彼らに上記のようなアドバイスをしたところ、ミスは減っていったという事実があります。
一方、下位層のミスは、かなり厄介です。
というのも、計算を含むミスを「単なるケアレスミス」と彼らは考えているからです。
それゆえ、彼らは「ちゃんと解けばミスはなくせる」と考えているようです。
(次回に続きます)
数学 トップ層のミスと下位層のミス ~その違い~ その3 2024/11/07
(前回の続きです)
学習苦手層の生徒さんは、計算ミスを指して、「凡ミス」という言葉をよく使います。
しかし、そのほどんどが「凡ミス」ではありません。
そして、「ちゃんとやれば」ミスはしなかったというような考えのようです。
彼らのミスを少なくする方法としては、こんな感じです。
・計算のルールを理解できていないがゆえのミス
→学習量が必要です。
すぐには改善しません。
・書いて計算せず、書かずに済ませてミス
→「とにかくきちんと書く」ことを何万回と指導
要するに、とにもかくにも学習量を増やしていくこと以外に方法はないと思っています。
しかも、気が遠くなるほどの。
そしてご留意いただきたいのは、ご父兄の中にも、
「やり方を教われば、我が子は少しずつできるようになっていくだろう」
とお考えの方が、意外といらっしゃることです。
しかし、これまでの経験では、こういうタイプの生徒さんに、やり方を教えても、ほぼ定着しません。
「ほぼ定着しない」ということは、「ほんの髪の毛一本分くらいは定着する」ということでもあります。
ゆえに、「何万回もの指導」が必要となってくるわけです。
ただ、わたしとしては、
「この生徒さんの学力なら、もう1問正解できたはず」
という「もう1問」をなるべく落とさない指導を引き続き心がけていきます。
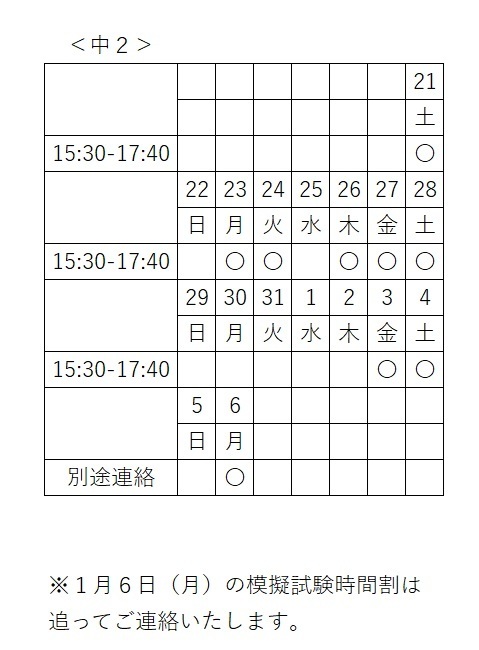
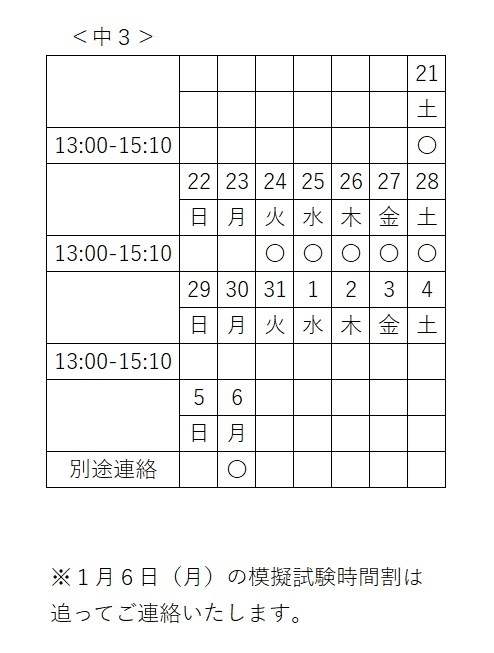
2024 冬期講習 実施要項 2024/11/08
表題の通り、冬期講習を以下の要領にて開催します。
塾生は原則全員参加です。
塾生には別途案内します。
塾生以外にも、興味のある方は、こちらまでご連絡ください。
◎講習は「頭を働かせ 手を動かす」
講習では、演習・自学時間を重視します。
下記の指導時間以外に、教室内で自学をしていただきます。
入試とは、制限時間内で、どのくらい頭を働かせ、手を動かすかを競うものです。
それゆえ、講習では、「頭を働かせ 手を動かす」時間をガッチリ取ります。
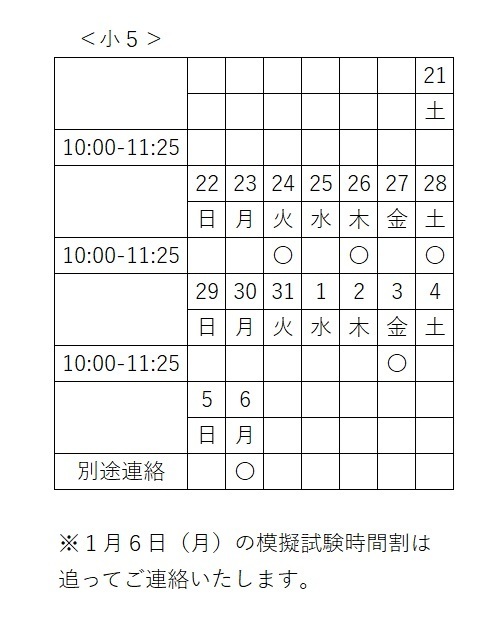
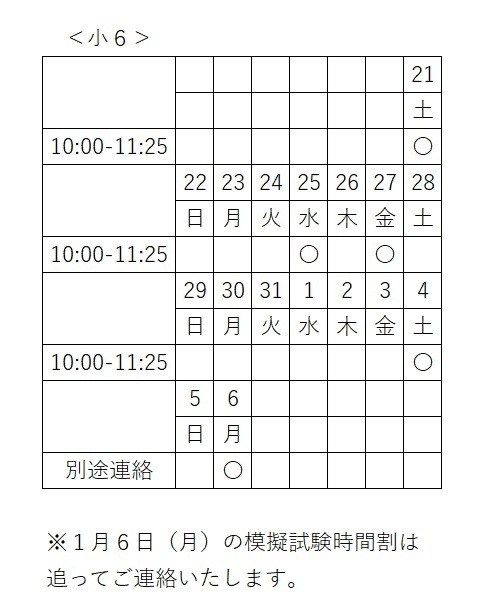
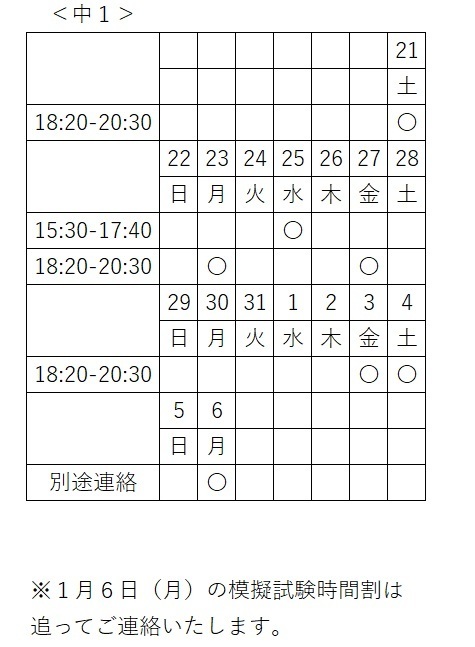
◎冬期講習日程
2024年12月21日(土)
~2025年1月6日(月)
☆この期間は冬期講習のみを実施いたします。
通常指導はありません。
☆1月6日(月)は模擬試験を実施いたします。
◎講習時間割
〇・・・講習実施日
◎料金
<冬期講習のみに参加の方>
☆いずれも税込み
小5・小6 15,130円
中1 18,980円
中2 19,800円
中3 21,270円
模擬試験代 3,000円
テキスト代 4,000円
<塾生の方>
別途案内します
中学生の受験学習 ~高校の授業をいかに意識してもらえるか~ その1 2024/11/09
わたしは、中学生の生徒さんの指導中によくこういう言い方をします。
...今、この単元でやっていることは、高校になると、○○という単元でその考え方の基本になります。
だから、この箇所は定期テストによく出るところなんです。
学校の先生方はそれが分かっていらっしゃる。
だから、この部分はこれこれこういう聞かれ方をするんです。
生徒さんは、わたしのこうした説明をふんふんと聞いています。
こういう説明をしだすと、「菊池の話は聞いておこうか」という気持ちが少し多くなるようです(笑)
つまり生徒さんの反応はよくなります。
受験学習において、「この先の学習にどうつながって行くか」を意識しておくことは非常に大切です。
わたしの指導では、こうした視点を特に重視しています。
確かに、わたしとしては、「今の単元・いま授業で扱っているところ」で、テストの点が良ければ、所期の目的は達成されます。
生徒さんにとっても、そうです。
しかし、生徒さんは高校に進んでも学習は続きます。
次のテストの点が良ければそれで終わりというものでもありません。
ゆえに、いま学習しているのが、今後にどうかかわってくるのか、知る限りのことを伝えておくことは、わたしの義務と考えています。
(次回に続きます)
中学生の受験学習 ~高校の授業をいかに意識してもらえるか~ その2 2024/11/10
(前回の続きです)
小中学校で学習するものの中で、わたしが「これは注意しておくべき」という単元があります。
それは次のような単元です。
・今のうちはできていなくても何とかやり過ごせる
・入試でもそこまで配点が高くない
・しかし、高校に行った途端、突然に大切になってくる
具体的に言うと、国語の文法なんかがそうです。
名詞・動詞・四段活用...とか言った内容のものです。
それから、数学というより算数で出てくる割合もそうです。
%の求め方などです。
国語の文法は、全般的に生徒さんの習熟度が非常に低いです。
それはトップ層もひっくるめてそうです。
高校入試であれば、せいぜい問題が出ても1問程度です。
点数にして3点程度でしょうか。
これが高校に進んだ途端、古文文法の基礎になります。
よって、この分野を理解していないと、あっという間に古文は分からなくなります。
%の求め方についても、同様です。
小5でやった%の求め方は、高校入試として必ずしも大きな比重を占めているとは言えません。
しかし、%の求め方を放置してしまっていると、高校に進んですぐ、理科の化学分野で入口の部分が皆目わからなくなってしまいます。
怖いことです。
(次回に続きます)
中学生の受験学習 ~高校の授業をいかに意識してもらえるか~ その3 2024/11/11
(前回の続きです)
高校入試において、塾の目標とするのは、
「志望校たる高校に合格すること」
です。
そのためにこそ、ご父兄は日々のお暮らしの中から、塾に授業料を支払います。
わたしはそれで生活しています。
しかし、わたしとしては、
「志望校たる高校に合格すること」
だけを目標としていません。
高校以降も学習は続きます。
むしろ、高校に入ってからのほうが、今までよりはずっと大変です。
そういった現状に対応できる力を今のうちからしっかり持っておくことは、高校入試突破と同じくらい大切です。
そして、そうした現状に耐えることができず、高校入学後に中退あるいは転校したというケースを、わたしはたくさん見てきました。
そういう生徒さんをこの目で見て、指導してきた経験からの発言です。
当然のことながら、中学生の生徒さんは、そのような現実を知りません。
よって、高校には高校での現実があること、そしてそれに対応できるように今のうちから意識するように促すことは、不可欠であるとわたしは考えています。
あとは、生徒さんが、わたしの話すことへどのくらい耳を傾けてくれるか、ということになります。
これが一番難しい!
高校受験の数学の問題は高校数学に役に立たない?? その1 2024/11/12
この間、とある学習塾の塾長さんがお書きになっているブログを拝見する機会がありました。
ブログの内容は、中高一貫校の生徒と、高校入試を受験する生徒との数学における違いです。
その塾長さんは、あらまし次のようなことをお書きになっていました。
・・・中高一貫校の生徒と、高校入試を受験する生徒を比べると、高校入試を受験する生徒の学習は無駄が多い。
中高一貫校の生徒は、数学に関して、公立中とは違う教科書を使って、ガンガン先取りをする。
それゆえ、そこで鍛えられた生徒は、難関大学の受験で、目覚ましい成果を出す。
一方、公立中の生徒は、高校入試を受ける必要がある。
そのため、中学のうちに、高校でやる数学の分野へ進むことができない。
高校受験の問題は、高校数学の分野で、あまり関係のない問題に重点を置かれる。
だから、高校受験の問題は、高校数学で役に立たない。
ここに書いてあることは、一点を除いて、わたしとだいたい同じ見解です。
ただ、最後の文章にある
「高校受験の問題は、高校数学で役に立たない」
というのには、
「そんなことはないと思うけどなあ」
というのが、正直なわたしの感想でした。
(次回に続きます)
高校受験の数学の問題は高校数学に役に立たない?? その2 2024/11/13
(前回の続きです)
高校受験の数学の問題は、大きく分けて、公立高校・国私立高校の2種類があります。
公立高校の入試は、全国の都道府県がそれぞれ実施しています。
東京ですと、一部例外はありますが。
そして、国私立高校は、学校ごとに問題を作成します。
問題の内容としては、公立高校より国私立高校のほうが難しいです。
事実、当県でも、入学難易度としてはそれほど高くない高校の入試問題でも、
「え? こういう難しい問題、出してるの?!」
ということは、意外にあります。
そして、中学数学の「メインイベント」、つまり関数・図形が絡んだ総合問題は、高校の数学を下支えしてくれます。
高校に入学した当初にやる数学は、高校入試でやった総合問題の恩恵はそれほど受けません。
しかし、高1も夏休みを過ぎたころになれば、高校入試で四苦八苦した難問・応用問題は、大切さを増してきます。
これが、高2・高3と学年が進めば、その存在はますます大きくなります。
特に、空間図形のような分野では、高校入試どころか、中学入試の問題が土台になっています。
ですから、
「微分・積分など小難しい計算は確かに高校の分野だが、基本的な考え方はまるまる中学入試」
といった問題も多いように感じます。
(次回に続きます)
高校受験の数学の問題は高校数学に役に立たない?? その3 2024/11/14
(前回の続きです)
高校受験を経ないでストレートに大学入試へ挑む中高一貫校
→例えば、二華・青陵など
高校受験を経て大学入試に挑む普通高校
→例えば、一高・二高など
どちらのカリキュラムがいいのかというのは、ご父兄にとって、なかなかに悩ましいです。
今回テーマにした
「高校受験の数学の問題は高校数学に役に立たないのか??」
というのも、見た目こそ違え、「中高一貫?or普通高校?」というのと同じ悩みです。
ただ、わたしの見るところ、「高校受験の数学の問題が役に立たない」と断言できるのは、中高一貫校のトップ層20%にあたる生徒さんくらいではないでしょうか。
彼らはいわゆる難関どころに行って、「○○高校の実績!」を形作る生徒さんたちです。
そういう「看板生徒」を除けば、高校受験の数学の問題がまるっきりのムダになってしまうということはない気がします。
それから、「高校受験の数学の問題」について、以下、ちょっと補足です。
高校受験を控えた中3生は、特にこれからの時期、数学の難しい問題にばかり気を取られてしまうと危険です。
大切なのは、
「基本となる問題を確実に得点する」
「易しい問題で失点しない」
ことです。
この点については、これまでも本欄で語ってきたことです。
また語らせていただきました。
中2生はダレる時期! ~さてどうするか~ その1 2024/11/15
こないだの中2生の授業のとき、こんな話をしました。
・・・中2の今の時期って、わたしから見てると、どうしてもダレる時期なんですよ。
たぶん、ダレている自覚はないと思いますが。
というのも、中2生は、中1のころと違って、「中学校っていうのは、どういうところか」というのが、十分に分かっています。
でも、3年生と違って、目の前に入試が迫ってきてるわけではない。
そうなってしまうと、ダレる人が出てくる。
公立高校入試は3月の初めころです。
でも、3年生は11月の終わりころには、内申評定、出ちゃうんです。
早いと思うかもしれませんが、1月の冬休みが明ければ、すぐに進路が決まる人もいますから。
中2生がダレる時期にあるというのは、中2生が少しゆったりした気持ちで勉強ができるっていうことです。
だから、この時期、例えば、入試向けの漢字の問題集・ボキャブラリー用の問題集・地理に出てくる地名など、
「自分でちょっと抜けてるなあ、ちょっと弱いなあ」
って感じるところを毎日少しずつでいいんで、学習してください。
こういうものって、少しずつでも続けていくのがいいです。
3年生になると、やらなきゃならないことがたくさんあって、とてもいま言ったような箇所をやれる気分にはなれませんよ。
(次回に続きます)
中2生はダレる時期! ~さてどうするか~ その2 2024/11/16
(前回の続きです)
前回のコラムで、わたしは生徒さんにあらまし、こう語りました。
「中2生はダレる時期にある」
「入試まで少し時間のあるこの時期、漢字・国語のボキャブラリー増強・地理に出てくる地名などの学習をしたほうがいい」
ここでわたしは、学習しておいたほうがいいものの実例を挙げました。
学習するのは、別にこれらに限定する必要はありません。
わたしがこの例を出したのは、空いた時間・隙間の時間・ちょっとボーとしているような時間にも、割と気軽に取り組めるからです。
それから、中2生を見ていますと、具体的な志望校をイメージとして描いている生徒さんは、少数派です。
また、中には成績から言って「途轍もない志望校」を口にする生徒さんもいます。
例えば、中2の12月のテストで、5教科200点に行かない、つまりどの教科も軒並み30点台という成績で、
「できれば一高に行きたいです。
最低でも学院高とか」
という生徒さんとか。
こういうことを言っている本人は、一高がどのくらいの難易度かなどということを、自分で調べようとした形跡もないし、自身の志望に向けて何か努力している風でもないのです。
志望校に具体的なイメージを持つことで、成績も改善する確率が高くなっていくことを、今のうちから中2生の方には覚えておいてほしいと感じています。
生徒さんは成績を上げたいと必ずしも考えない でもね... その1 2024/11/17
今回のコラムは、主として、わたしの「愚痴吐き」です。
何か、受験のためになることは、何も書きません。
以下、お読みになる方は、この点をご了承ください。
さて、受験指導をしていると、生徒さんの様子から見えてくることが随分とあります。
学習塾というのは、言うまでもなく、生徒さんの受験学習の補助・補強です。
それは生徒さんも分かっています。
そして、そうした受験学習の補助・補強は、生徒さんのほうで、
「なんとかできるようになりたい!」
「できるようになるには、しっかり努力する!」
というマインドを全員が持つようになれば、今ほど苦労はしません。
ところが、実際のところ、
「生徒さんは成績を上げたいと必ずしも考えないものだ」
というのが、よく伝わってきます。
「あなたは成績上がったほうがいいですか?」
生徒さんにこう尋ねると、多くの生徒さんは「はい」と答えます。
「できれば」
「まあ」
という回答もあります。
要するに、程度の差こそあれ、
「成績を上げたい」
とは、考えているようです。
しかし、
「そのために、何か自分で積極的にこれこれのことをやっていますか?」
と問うと、彼らは途端に口ごもります。
歯切れが悪くなります。
それが現実というものでしょう。
(次回に続きます)
生徒さんは成績を上げたいと必ずしも考えない でもね... その2 2024/11/18
(前回の続きです)
彼らの受験指導に当たっていると、あることに気づきます。
それは、「面倒なことはできる限りやりたくない」ということです。
これは振り返ってみると、わたしも同じです(笑)
面倒なことをやりたくないのは、学習に限らずです。
ただ、その「面倒なこと」を避けてしまったため、後々もっと面倒な事態・困った事態になってしまうということも「よくある話」ではあります。
例えば、書類の整理をちょっとの間に怠ってしまうなど。
その結果、必要な書類が行方不明になるという経験をする羽目になります。
大人になれば、子供時代に比べて、理性が働きます。
もっとも、その「理性の度合い」は人によるわけですが...
ともあれ、「面倒なことはできる限りやりたくない」を続けると、かえって面倒になるということは、大人になれば、経験上分かっているわけです。
ところが、後々の面倒なことに苦しむより、目先の面倒なことを避けてしまう気持ちがまさっている生徒さんが、非常に多いです。
高校生くらいになると、さすがに理性のきき始める生徒さんが多くはなります。
中学生あたりですと、特に男子生徒は、女子生徒に比べて、未熟なケースが多いです。
(次回に続きます)
生徒さんは成績を上げたいと必ずしも考えない でもね... その3 2024/11/19
(前回の続きです)
「面倒なことはできる限りやりたくない」
「後々もっと面倒な事態・困った事態になってしまうより、目先の手抜きを選ぶ」
そういう生徒さんがかなり多いという現状を考えると、そこに成績アップのヒントがあります。
「仕事を今よりほんの少しだけ丁寧にするように心がける」
実はこれだけで、成績は今よりほんのちょっとだけ改善します。
「ほんの少し」って、どのくらい?
例えば、テストで1問分、3点くらいとか。
「たったの3点かよ」
そう思うかもしれません。
でも、それが入試と絡むと、5教科で、15点プラスです。
15点プラスと言えば、高校受験の場合、偏差値2の違いです。
ただ、「仕事を今よりほんの少しだけ丁寧にするように心がける」というのは、簡単そうで、実に難しいです。
簡単にできるようであれば、誰もがもうやっているでしょう。
希少価値はそこになくなります。
ですから、いまわたしが申しあげたことを、心にとめて、実行してほしいのです。
そして、それを実行した生徒さんは、成績アップという結果を残しています。
もちろん、わたしはこういう生徒さんを応援します。
今回のコラムは、何だかグダグタでした。
前々回述べたように、わたしの単なる愚痴でした。
いろいろと済みません。
高校受験 偏差値55以上の中3生へ「入試は難問で差がつかない」 その1 2024/11/20
昨日、ついに当地では初雪が降りました。
こういう時節になると、高校入試では、過去問演習をしている中3生が次々と出てきます。
この時期、すでに過去問演習に入っている受験生となると、多くは偏差値55以上の生徒さんたちでしょうか。
この過去問演習をするに当たり、心にとめておいてほしいことを述べてみます。
対象とするのが、偏差値55以上の中3生です。
今回のコラムで、わたしが焦点を当てたいのが、難問についてです。
そして、
「難問に関わり過ぎるな!」
「難問にハマリすぎると時間ばかり食ってしまう!」
ということをお伝えしたいのです。
このレベルの生徒さんですと、間違った問題・分からなかった問題への対応は何とかこなせるはずです。
そうした中で、
「これならもうちょっと頑張れば解けたはず」
というものがあります。
一方で、
「これってどうやって解くの?」
「この問題、絶対に無理だわ」
というようなものにもぶち当たります。
これは自分にとっての「難問」です。
例えば、数学の入試の最終問題に出てくるようなものを思い浮かべていただくと、イメージがつかめます。
そうした「難問」に時間を取られ過ぎると、大変なことになります。
いくら時間があっても足りません。
(次回に続きます)
高校受験 偏差値55以上の中3生へ「入試は難問で差がつかない」 その2 2024/11/21
(前回の続きです)
過去問演習が始まる時期になると、生徒さんから
「これって解説を読んでもよく分かりません」
という質問が寄せられます。
その多くは、数学の難問です。
そして、偏差値55以上の中3生は、そういう問題に当たったとき、長い時間をかけて考え込んでしまうのです。
もちろん、考えることは大切です。
問題を見ただけで、考えもせず、放棄してしまっては力が付きませんから。
しかし、あまりに自分の実力からかけ離れた問題にハマってしまうと、受験学習としては、マイナスになってしまいます。
入試は合格することが目的です。
満点を取ることが目的ではありません。
そして、入試は難問で差がつきません。
差がつくのは、自分が受ける高校の受験生であれば、当然に解けるはずの問題を落としてしまったときです。
事実、みやぎ模試などの正答率を見ていますと、あることに気づきます。
それは、偏差値70超え、つまり二高B70%が出るような生徒さんでも、正答率50%以上の問題を全問正解しているという生徒さんは、意外といないことです。
ということは、そのクラスの生徒さんにして、取りこぼしがあるということです。
ですから、自分の能力を遥かに超えた難問は、「やるべきことをやった上で捨てる勇気」を持ってほしいのです。
(次回に続きます)
高校受験 偏差値55以上の中3生へ「入試は難問で差がつかない」 その3 2024/11/22
(前回の続きです)
難問ということに関して言うと、過去問集にある問題解説は、必ずしも分かりやすく書いているとは言えません。
「全国高校入試問題正解」=(いわゆる「電話帳」)は、紙面の都合でやむを得ないにしても、かなり荒削りです。
東京学参が出している学校別の過去問集でも、「電話帳」よりは親切ながら、それでも毎年、難問に関する質問が来ます。
その解説には、かなりの時間を要します。
そんなこともあって、生徒さんには、
「この問題は、あなたにとって難しすぎるので、答え合わせをカットしてもらっていい」
「その代わり、この部分のこの式の導き方は、今後も出るかもしれないから、ここはしっかり身につけておいてください」
というようなことは、生徒さんに伝えます。
前回のコラムで、自分の能力を遥かに超えた難問は、「やるべきことをやった上で捨てる勇気」を持ってほしいと言いました。
ここで大切なのは、「やるべきことをやった上で」という箇所です。
深く考えもせず、ちょっと難しそうだからと考えを放棄しては、何のための演習か分からなくなります。
さすがに偏差値55以上の中3生ともなれば、そのあたりのことは理解するでしょう。
一応、老婆心ながら、ということで記しておきます。
この頃の中学生の学力は低下したのか? その1 2024/11/23
「この頃の中学生の学力は低下したのではないか」
塾の先生など、ご同業の方々がしばしばこのようなフレーズをネットにて発信なさっているようです。
この件について、「中学生は以前に比べて、ホントに学力が低下してしまったのか」というのを、わたしなりの視点で考えてみます。
ただ「以前の中学生」といっても「どのくらい『以前』なの?」という疑問は当然あります。
ここでは便宜的に「20年くらい前」としておきます。
さて、中学生の学力を巡って、わたしの感じているのは、次の通りです。
1.今の中学生は、「以前の中学生」に比べて、学力が下がったかどうかはハッキリ断言できない
2.今の中学生は、「以前の中学生」に比べて、学力の格差は大きくなっている
3.今の中学生は、「以前の中学生」に比べて、学力が上がっているケース・下がっているケースが同じくらいいるのではないか
わたしはこれまで、どちらかというと、学力に難のある生徒さんを多く見てきました。
学習の苦手な生徒さんは、いつの時代にもいます。
それは、「以前の中学生」だろうが、「今の中学生」だろうが、変わりはありません。
学習の「苦手の度合い」は、以前と今とで、それほど大きくはないのではないかというのが、わたしの見立てです。
(次回に続きます)
この頃の中学生の学力は低下したのか? その2 2024/11/24
(前回の続きです)
では、なぜ塾の先生など、ご同業の受験関係者の方が、
「この頃の中学生の学力は低下したのではないか」
とお感じになるのか。
理由として考えられるのは、
「若いころに比べて、ご自身がスキルアップしたため、生徒さんの『あら』がよく見えるようになった」
ということです。
受験指導を長くやっていれば、指導経験の量は多くなります。
そのため、
「昔は気づかなかったことに、今更ながらこういう点に気づいた」
というようなことはあります。
それから、塾の場合、
「20年くらい前なら塾に通わなかった『学習苦手な層』が、塾に通うようになった」
という側面も影響している可能性があります。
少子化の影響で、親が子供1人当たりに使う金額が多くなりました。
その結果、「学習苦手な層」の生徒さんたちを、20年くらい前より多く目にするようになっている面も否定できません。
ご自身のスキルアップと、「学習苦手な層」を多く目にするようになった結果、
「20年くらい前はこんなんじゃなかった」
「昔の生徒はもっとできていた」
と感じるようになっても不思議ではありません。
何しろ、わたしが中高校生時代から、
「今の子供たちは昔にはなかったテレビを見るようになって、学力・国語力が低下した」
などと、言われていましたから。
(次回に続きます)
この頃の中学生の学力は低下したのか? その3 2024/11/25
(前回の続きです)
ただ、割とハッキリしていることがあります。
それは、中学生間の学力格差が以前に比べて大きくなってきていることです。
学力は、昔から生徒間で格差はあります。
それを点数ごとに並べていくと、だいたい↓のようなグラフになっていました。
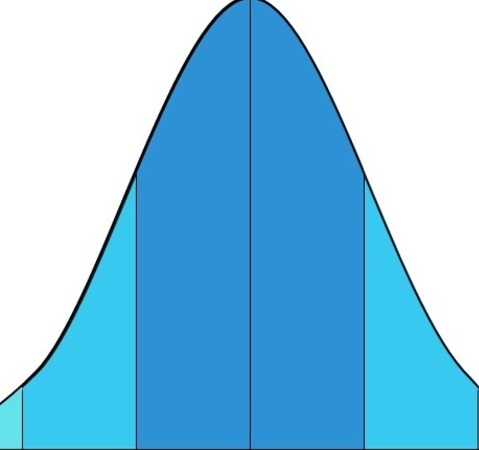
このようなグラフを目にしたことのある方は多いでしょう。
こういう格差は「健全」なものです。
ですから、生徒間でこのような格差があっても、特に大きな問題にはなりません。
ところが、いま、生徒の成績は次のような図になることがあります。
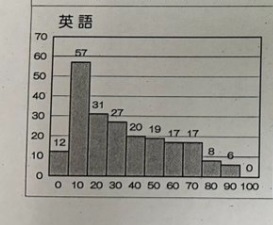
上に示したものは、Twitter上に上がっていたものです。
中3の2学期末試験の度数分布表です。
さすがにここまで極端なのは、なかなか目にすることはありません。
この試験の5教科総合ですと、↓のようになります。
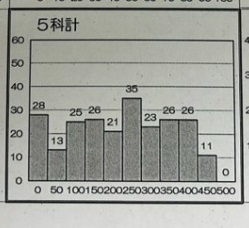
このパターンは、ときどき見かけます。
この図を見ると、真ん中がほんの少しだけ多くなっています。
それ以外は、点数ごとの人数がほぼ同じです。
ということは、以前は真ん中あたりに集中していたものが、真ん中の部分がへこんでしまったわけです。
真ん中がへこんだということは、「中間」にいた層が少なくなってしまったということです。
生徒間の格差が広がっているというのは、そういう意味です。
(次回に続きます)
この頃の中学生の学力は低下したのか? その4 2024/11/26
(前回の続きです)
前回のコラムで、生徒間の成績格差が大きくなっていると述べました。
そして、「真ん中」が減り、減った分が平らになっている事実も示しました。
ここで、一つ思い当たることがあります。
それは、「真ん中」が減って、全体的に平らな人数分布になっているとしたら、
「学力が低下した生徒と同じくらい、上昇した生徒もいるのではないか」
ということです。
なぜ彼らは上昇したのか。
例えば、以前20年ほど前であれば塾通いをしなかった生徒さんが通塾によって、底上げがされたとか。
明確な理由は分かりません。
しかし、そうとでも考えないと、「平らな人数分布」の説明がつかない気がしています。
では、受験関係者からなぜ「アップした層」のことが語られないのか...
たぶん、「下がった部分」は「上がった部分」に比べると、目につきやすいことが、原因になっているのではないかと、わたしは推測しています。
そして、今後、ますますの少子化で、この格差が小さくなることがないであろうとも、考えています。
よって、上位層は、難関を目指すために、引き続きハードな受験学習を続けていかなくてはならないでしょう。
逆に下位層はあまり勉強しなくてもよくなっていく状態が加速していくでしょう。
いいことなのか、よくないことなのか...
偏差値55以上の高校の高1生へ ~学校がつらくなったら読んでね!~ その1 2024/11/27
今回は、偏差値55以上の高校の高1生へ向けたコラムです。
その中でも、学校がつらくなった方、学校の勉強がよく分からなくなってしまった方を思い浮かべながら書きます。
さて、高1生の多くは定期試験の季節になってきています。
定期試験は、高校入学以来、都合3回目です。
前回9月の定期試験あたりで、かなり日々の学習がつらくなってしまった方もいるはずです。
そして、今回また試験...
「何とか赤点回避」だけなら、まだ救いはあります。
これが高じてくると、不登校になったり、不登校になると授業がますます分からず...という悪循環になります。
そして、この悪循環の果ては、今の学校を辞めてしまうということになりかねません。
この件に関しては、以前にYouTube動画・当コラムで、↓のような発信をしています。
<関連リンク>
学校を辞める理由は、学習面だけではないかもしれません。
しかし、何だかんだで、中退する大きな理由は、
「勉強について行けなくなった」
という点です。
(次回に続きます)
偏差値55以上の高校の高1生へ ~学校がつらくなったら読んでね!~ その2 2024/11/28
(前回の続きです)
偏差値55以上の生徒さんというのは、たぶん小中学校を通じて、
「勉強が分からなくなってしまった」
という経験をしたことのない人がほとんどです。
なぜなら、この成績層の生徒さんは、公立の小中学校であれば、全体の上位3分の1くらいまでにはいたからです。
ですから、高校に入って、何らかの理由で勉強が分からない、授業について行けなくなったとき、どうしたらいいのか、分からなくなってしまうのです。
一度、何かのきっかけで学習に対する意欲がなくなってしまうと、それを取り戻すにはかなりの労力が必要です。
そして、結果として学校を辞めることになっても、本人の選択によるもの、と片づけてしまってもいいのかもしれません。
しかし、もし「できれば学校を辞めたくない」と考えているのであれば、
「いまよりは少し授業が分かるようになる」
「テストの点が良くなる」
必要があります。
これをやるためには、一つ方法があります。
それは「数学を教科書からやり直してみる」ことです。
「教科書からやり直してみる」というのは、
・教科書ガイドを使って
・数学の教科書の例題・練習問題を解いていく
・最低3回繰り返す
という方法です。
(次回に続きます)
偏差値55以上の高校の高1生へ ~学校がつらくなったら読んでね!~ その3 2024/11/29
(前回の続きです)
教科書ガイドを使って、数学の教科書をやり直してみるというのは、確かに大変です。
しかし「何をやったらいいか分からない状態」で、数学から手を付けてみるというのは、次のような利点があります。
・数1・数Aの最初のほうに戻っても、そこまで分量は多くない
・偏差値55以上の生徒さんなら教科書の問題の独習は可能
・数学はあらゆる教科の中で記憶すべき量が最も少ない
・「今後自分は何とかやれるかもしれない」と最も感じさせてくれる教科は数学
数学が分からなくなっていても、すべてがまるっきり抜けているという人は少ないでしょう。
数1ならば二次関数あたりから段々怪しくなっていく人が多いはずです。
偏差値55以上の生徒さんは、中学までの数学なら「まずまず何とかなった」はずです。
であるなら、数学の教科書の最初のほうに戻るといっても、絶望的な量ではありません。
「ここは分かっている」ということであれば、サラッとやるくらいでもいいでしょう。
ただ、ほんとうに分かっているかどうかは、
「問題が自力で解けるかどうか」
で判断しなくてはなりません。
自力で解けないとしたら、その箇所は、あくまで「分かっていたつもり」でしかありません。
(次回に続きます)
偏差値55以上の高校の高1生へ ~学校がつらくなったら読んでね!~ その4 2024/11/30
(前回の続きです)
「数学が少しでも分かるようになってくると、学校へ行く気力が少し湧いてくる」
というのは、過去にそうした事例があります。
家庭教師として個別指導をしていたころ、何名か不登校寸前の生徒さんを担当したことがあります。
偏差値55以上の高校の高1生です。
彼らは「何からどう手をつけていいのか分からない」といった風でした。
そこで、数学のやり直しをやると、彼らの気力はわずかずつ改善していきます。
特に「教科書にある練習問題を繰り返す」というのは、意味があるようです。
また、数学の指導ということに関しては、中学生で定期試験5教科100点±30点くらいの生徒さんを個別指導で教えたときにもやった方法です。
英語あるいは他の教科ですと、「覚えなくてはならないこと」が盛りだくさんです。
その点、数学は「地道に独習していけば、赤点は回避できる」教科です。
そして、逆の視点でいうと、「教科書の最初のころに戻って教科書ガイドを使いながら数学を学習する」ことができないほど気力がないのなら、高校中退する確率は大きいと考えていただきたいのです。
もしわずかでも、「中退するのはなるべく避けたい」という気持ちがあるなら、今まで述べたこと、実践してみてください。
何らかの活路は見いだせると思います。
ご利用案内 リンク
お気軽にお問合せください

メール・お電話でのお問合せ
<電話での受付>
15:00~20:00
※日曜日は除く
※電話は
「雅興産(みやびこうさん)」と出ます
成績upのヒント!
教育コラム「雨か嵐か」
プロ家庭教師菊池
住所
〒981-0933
仙台市青葉区柏木1-2-29-301
電話受付時間
15:00~20:00
定休日
日曜日